Fact Fluency and Memorization
|
"Fact fluency" is the ability to rapidly answer an addition, subtraction, multiplication or division problem involving single digits quickly and without great effort.
Typically, students are expected to be fluent with addition facts up to 10+10, subtraction within 20, multiplication facts up to 12x12, and division facts up to 100÷10. Students meet these benchmarks throughout their K-5 education. (Students are expected to be fluent with addition and subtraction facts by the end of 2nd grade, multiplication facts by the end of 4th, and division facts by the end of 5th.) Some students find it 'easy' to memorize these facts. For others, memorization seems an arduous task -- and in turns out that forced memorization may, in fact, hinder them in later mathematics. StrategiesAddition + Subtraction
-- Count on/Count Back 1, 2, 3 -- Double -- Double +1, -1 -- Make a 10 Multiplication and Division -- Doubling and Halving -- Breaking down into known facts Work to Understand the Why MORE COMING SOON -J. Laib, 2015 |
Articles
Assessing Basic Fact Fluency, by Gina Kling and Jennifer M. Bay-Williams
published in the April 2014 edition of NCTM's Teaching Children Mathematics Interested in continuing the conversation about fact fluency? Talk to one of Driscoll's math specialists, Jenna Laib or Stephen Buck, or your child's classroom teacher! | ||
Conceptual Multiplication Flashcards
Subitizing
These cards involve subtilizing, which is the ability to determine a quantity without counting one by one. In the example above, there are 7 groups of dots (5 groups at the bottom and 2 at the top makes 7 groups in all). Each circle contains 7 dots (6 dots + 1 on the side).
7 groups of 7 = 49. A student might see this as 5 groups of 7 (35) + 2 groups of 7 (14) = 7 groups of 7, or 49. Another student might see all the sixes and say 7 groups of 6 = 42, and then 1 more in each of the 7 groups adds another 7. 42 + 7 = 49. cards courtesy of Graham Fletcher. |
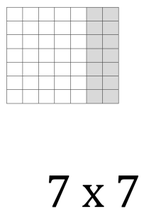
Arrays
Each of these cards features the multiplication fact modeled as an array (ordered into organized rows and columns). Many of the cards also emphasis "friendly" groups, like rows of 5.
For example, to solve 7 x 7, one might do 7 rows of 5 (7x5=35) and then 7 rows of 2 (7x2=14), and combine them to get 7 rows of 7 = 49. 35 + 14 = 49 cards courtesy of Graham Fletcher. | ||||